go --- 最大堆和最小堆

最大堆（大顶堆）：堆顶元素保持最大

最小堆（小顶堆）：堆顶元素保持最小

1、堆的结构

  堆是一种完全二叉树（完全二叉树是满二叉树的一部分），根据树的结构可以通过数组来进行表示，如下图中的完全二叉树可以表示为右侧的数组

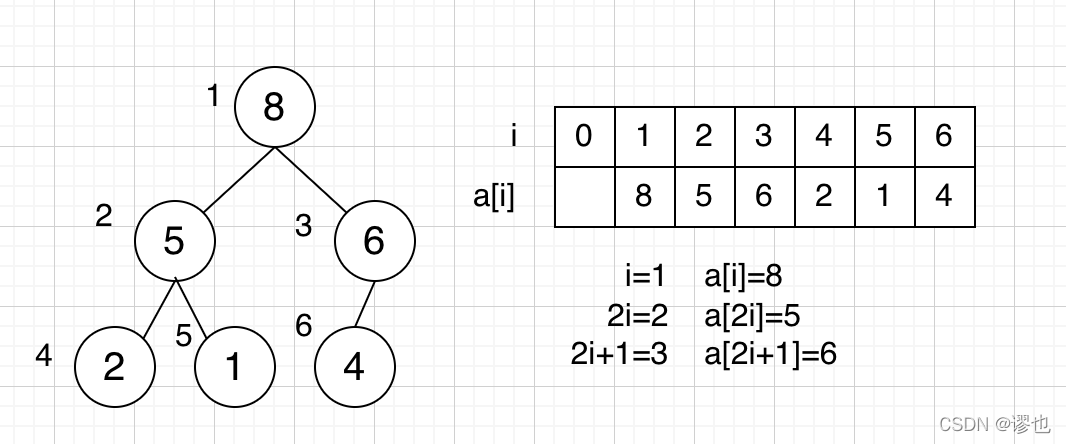
作为大顶堆时，还需遵循以下特性：

1. 根节点为整个堆的最大值
2. 每个节点的值都不小于它的子节点

对应到数组中：

1. a[1]为最大值

2. 节点为i，则子节点为2i和2i+1，即a[i]>=a[2i] && a[i]>=a[2i+1]

3. 节点为i，则父节点为i/2

2、向堆中插入元素

插入新元素时，需要寻找其在数组中的位置

//less()比较元素大小，exch()交换两元素位置
func push(k int, datas *[]int){
   for i>1 && less((*datas)[i/2],(*datas)[i]){   //比较i/2和i位置元素的大小，比较至根节点时退出
       exch(&(*datas)[i/2], &(*datas)[i])   // i/2位置元素小于i位置元素，说明父节点元素小于子节点，需要交换
       i = i/2
   }
}

func less(a int,b int) bool{
	return a < b
}

3、弹出堆中元素

弹出最大元素，将最后一个元素与最大元素交换，然后调整此时最后一个元素的位置到正确的位置

func pop(i int, datas []int){
    length:=len(datas)-2
    for 2*i<=length{
        max:=0
        if 2*i<length && less(datas[2*i], datas[2*i+1]){  //找两个子节点2i和2i+1中的最大值
            max=2*i+1
        }
        if !less(datas[i], datas[max]){  // 父节点大于子节点，交换结束
            break
        }
        // 子节点大于父节点，交换
        exch(&datas[i], &datas[max])
        i = max
    }
}

4、go中的堆

go中提供了 container/heap 来实现堆，堆中元素的类型需要实现 heap.Interface 这个接口。

下面是最大堆示例：

type IntHeap []int

func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }
//最小堆
//func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IntHeap) Push(x interface{}) {
	*h = append(*h, x.(int))
}
func (h *IntHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}


func main()  {
	h := &IntHeap{3, 1, 2, 5}
	heap.Init(h)
  heap.Push(h, 4)
	for h.Len() > 0 {
		fmt.Printf("%d ", heap.Pop(h))
	}
}

 
如有不对，烦请指出~