树:用于描述一对多的数据关系
二叉树的定义
二叉树(BinaryTree)是n个有限结点的有限集合,集合可为空,或由根节点和两科互不相交的子树构成,其子树也是二叉树,因此二叉树具有递归结构。
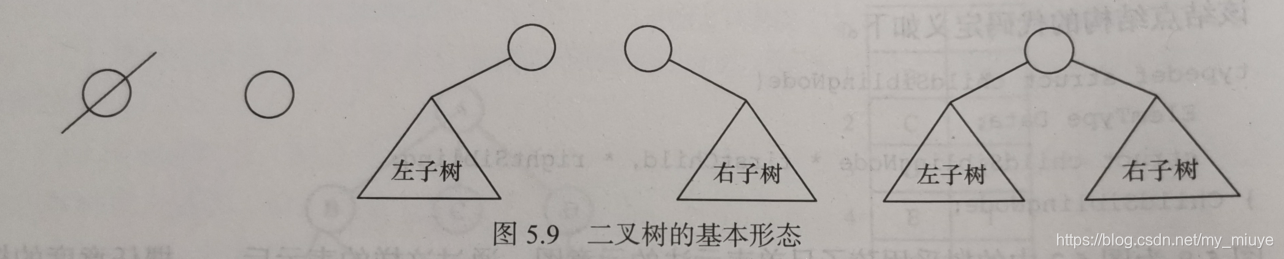
二叉树的基本形态:
二叉树的性质:
1.在二叉树的第i层上至多有 2i-1 个结点(i ≥ 1)。
2.高度为h的二叉树上最多有2h-1个结点(h≥1)。
3.任意一棵二叉树中,若叶子结点的个数为n0,度为1的结点的个数为n1,度为2的结点的个数为n2,则有n0=n2+1。
4.包含n个结点的二叉树的高度值最小为┍ log2(n+1) ┑(向上取整),最大为n。
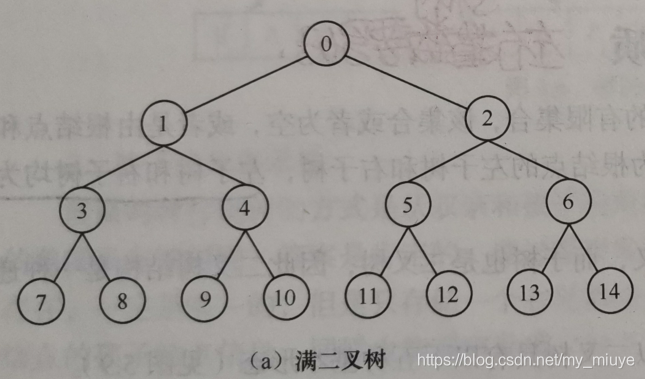
满二叉树:
在一颗二叉树中,所有的叶子结点都在二叉树的同一层上,除了叶子结点外,所有的分支结点都有两棵子树,这样的二叉树称为满二叉树。
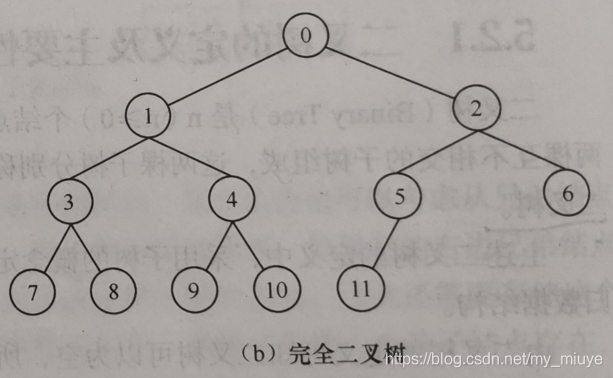
完全二叉树:
只有最下面两层结点的度可以小于2,且最下面一层的叶子结点编号连续集中在靠左的位置上的二叉树成为完全二叉树。
假定对一棵有n个结点的完全二叉树中的结点,按层次从上到下、每层结点从左到右的顺序,从0到n-1编号(如上图),设图中某个结点的编号为i,则有
1)当i=0,该结点无双亲,为二叉树的根;当i>0时,该结点的双亲结点编号为└ (i-1)/2┘(向下取整)
2)若 2i+1<n,则其左孩子存在并且其编号为2i+1;否则该结点无左孩子
3)若 2(i+1)<n,则其右孩子存在并且其编号为2(i+1);否则该结点无右孩子
**满二叉树一定是完全二叉树,反之不然