【数据结构】二叉树的前序、中序、后序、层次遍历

二叉树的遍历：
   二叉树的遍历是指按照某种次序对所有结点进行访问且每个结点只被访问一次的操作。因为二叉树具有递归结构，因此可用递归进行遍历。

先序遍历：

• 若二叉树为空，则空操作返回
• 否则，访问根结点，再先序遍历左子树，然后先序遍历右子树

对于一个先序序列，根结点一定是序列的第一个

 void PreorderTraversal( BinTree BT ) 
 {     
 	if( BT ) {
 	         printf("%d ", BT->Data );         // 此处假设对BT结点的访问就是打印数据，并假设数据为整型
 	         PreorderTraversal( BT->Left );
 	         PreorderTraversal( BT->Right );
 	          }
  } 

中序遍历：

• 若二叉树为空，则空操作返回
• 否则，先中序遍历左子树，再访问根结点，然后中序遍历右子树

对于一个中序序列，根结点在序列的中间，根结点左边的序列为左子树，右边的序列为右子树
  （特殊情况：只有右子树时，根结点在第一个）

void InorderTraversal( BinTree BT ) 
{    
	 if( BT ) {
	          InorderTraversal( BT->Left );                
	          printf("%d ", BT->Data);  
	          InorderTraversal( BT->Right );
	          } 
 } 

后序遍历：

• 若二叉树为空，则空操作返回
• 否则，先后序遍历左子树，再后序遍历右子树，然后访问根结点

对于一个后序序列，根结点一定在序列的最后一个

  void PostorderTraversal( BinTree BT )
   {    
   		 if( BT ) {        
   		  PostorderTraversal( BT->Left );        
   		  PostorderTraversal( BT->Right );         
   		  printf("%d ", BT->Data);     
   		  } 
  }

层次遍历（广度优先）：

• 从队列中取出一个元素；
• 访问该元素
• 若该元素所指结点的左、右孩子节点非空，则将其左、右孩子的指针顺序入队

void LevelorderTraversal ( BinTree BT ) 
{      
	Queue Q;      
	BinTree T;    
	 if ( !BT ) return; /* 若是空树则直接返回 */          
	 Q = CreatQueue(); /* 创建空队列Q */     
	 AddQ( Q, BT );     
	 while ( !IsEmpty(Q) ) {         
	 	T = DeleteQ( Q );        
	 	 printf("%d ", T->Data); /* 访问取出队列的结点 */         
	 	 if ( T->Left )  
	 	 	 AddQ( Q, T->Left );         
	 	 if ( T->Right )  
	 	 AddQ( Q, T->Right );     
	 	 }
 }

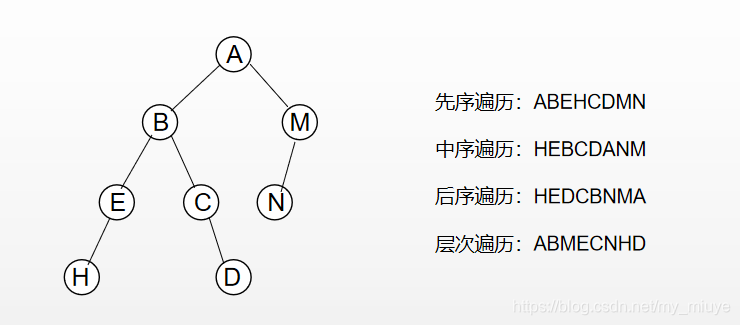
然后我们举个栗子来形象化理解一下：

*先序序列和中序序列可以唯一确定一棵二叉树
*后序序列和中序序列可以唯一确定一棵二叉树

*先序序列和后序序列不能唯一确定一棵二叉树
 

中序遍历非递归遍历算法：

• 先根节点入队；
• 遇到一个结点，就把它压栈，并去遍历它的左子树；
• 当左子树遍历结束后，从栈顶弹出这个结点并访问它；
• 然后按其右指针再去中序遍历该结点的右子树。

void InOrderTraversal(BinTree BT)
{
	BinTree T = BT;
	Stack S = CreateStack(MaxSize);      //创建并初始化堆栈S
	while(T||!IsEmpty(S)){
		while(T){            //一直向左并将沿途的结点压入堆栈
			push(S,T);
			T = T->Left;
		}
		if(!IsEmpty(S)){
			T = Pop(S);          //将结点弹出堆栈
			printf("%5d",T->Data);         //打印结点
			T = T->Right;         //转向右子树
		}
	}
}

部分参考自浙江大学数据结构慕课